내분점 외분점 공식! 차이점 완벽정리

안녕하세요, 여러분!
오늘은 수학에서 중요한 두 가지 공식,
내분점 공식과 외분점 공식에
대해 알아보겠습니다.
이 두 공식은 좌표 계산에서
핵심적인 역할을 하는데요,
특히 선분을 특정 비율로 나누거나
연장할 때 사용됩니다.
내분점 공식이란?
내분점 공식은 선분을 특정 비율로
나누는 점의 좌표를 구하는 데 사용됩니다.
두 점 A(x₁, y₁)와 B(x₂, y₂)가 있고,
이 선분을 m:n의 비율로 나누는 점
P의 좌표를 구하고 싶다면
다음 공식을 사용합니다.
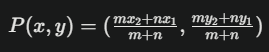
이 공식은 선분 내부에서
점을 찾는 데 사용되며,
다양한 기하학적 문제를 해결하는 데
매우 유용합니다.
외분점 공식이란?
외분점 공식은 선분을
특정 비율로 연장하여
나누는 점의 좌표를 구하는 데
사용됩니다.
두 점 A(x₁, y₁)와 B(x₂, y₂)가 있고,
이 선분을 m:n의 비율로 외분하는 점
Q의 좌표를 구하고 싶다면
다음 공식을 사용합니다:
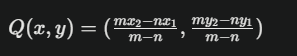
이 공식은 선분 외부에서
점을 찾는 데 사용되며,
특히 확장된 기하학적 문제에서
중요한 역할을 합니다.
내분점 공식과 외분점 공식의 주요 차이점
두 공식의 차이점을 명확히 이해하는 것은
수학 문제 해결에 큰 도움이 됩니다.
주요 차이점을 살펴볼까요?
위치
내분점 공식은
선분 내부의 점을 찾는 데 사용되고,
외분점 공식은
선분 외부의 점을 찾는 데 사용됩니다.
계산 방식
내분점 공식은 비율의 합(m+n)을 사용하지만,
외분점 공식은 비율의 차(m-n)를 사용합니다.
활용 사례
내분점 공식은
삼각형의 무게중심 계산 등에서 사용되며,
외분점 공식은
외접원 중심 계산 등에서 활용됩니다.
내분점과 외분점 공식을 활용한 예제
이론만으로는 이해하기 어려울 수 있으니,
실제 예제를 통해
두 공식의 사용법을 알아보겠습니다.
예제 1: 내분점 공식 활용하기
점 A(2, 3)과 B(8, 7)을
2:3의 비율로 나누는
점 P의 좌표를 구해봅시다.
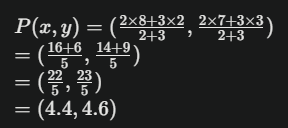
이렇게 내분점 공식을 사용하면
선분 AB를 2:3으로 나누는 점 P의 좌표를
정확히 구할 수 있습니다.
예제 2: 외분점 공식 활용하기
점 A(1, 2)과 B(4, 6)을
1:2의 비율로 외분하는 점
Q의 좌표를 구해봅시다.
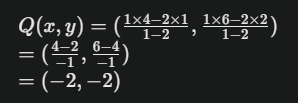
이렇게 외분점 공식을 사용하면
선분 AB를 1:2로 외분하는 점
Q의 좌표를 정확히 구할 수 있습니다.
내분점 공식과 외분점 공식은
좌표 기하학에서 매우 중요한 도구입니다.
내분점 공식 실생활 활용 사례! 이렇게 활용됩니다
여러분은 학창 시절 수학 시간에 배운 내분점 공식을 기억하시나요? 많은 사람들이 이 공식을 단순히 시험을 위해 암기했다가 잊어버리곤 합니다. 하지만 이 공식은 우리 일상 곳곳에서 활용
ceomorningbird.tistory.com
내분점 공식 완벽 이해하기 ! 기초부터 활용까지
내분점 공식이란? 내분점 공식은좌표 기하학에서 중요한 개념으로,두 점 사이의 특정 비율에 따라점을 나누는 방법을 설명합니다. 이 공식은 수학 공부를 하는 학생들에게필수적인 도구로,실
ceomorningbird.tistory.com
'정보글' 카테고리의 다른 글
| 배낭여행 필수품! 꼭 챙겨야 할 해외여행 준비물 체크리스트 (0) | 2024.12.08 |
|---|---|
| 크리스마스 영화 추천 17선! 애니메이션, 클래식 코미디 등 (0) | 2024.12.08 |
| 내분점 공식 실생활 활용 사례! 이렇게 활용됩니다 (0) | 2024.12.07 |
| 내분점 공식 완벽 이해하기 ! 기초부터 활용까지 (0) | 2024.12.07 |
| 니거(니가) 뜻과 유래! 영원한 금기? 니가의 현재 사용 의미까지 (0) | 2024.12.07 |




댓글